Jiao and Pretis Outlier Proportion and Count Tests

Tests whether the proportion (or number) of outliers detected using impulse indicator saturation is different from the proportion (or number) of outliers expected under the null hypothesis of no outliers using the Jiao and Pretis (2019) proportion and count outlier tests.

Usage

outliertest(x, noutl=NULL, t.pval=NULL, T=NULL, 
  m=1, infty=FALSE, alternative="two.sided")

Arguments

x: an isat object
noutl: integer, number of detected outliers if no isat object is provided i.e. x=NULL
t.pval: numeric, between 0 and 1. Selection p-value used in indicator saturation if no isat object is provided i.e. x=NULL
T: integer, sample sized used in indicator saturation if no isat object is provided i.e. x=NULL
m: integer, number of iterations in variance computation, default=1
infty: logical, argument used for variance computation
alternative: "two-sided", "less", "greater", alternative hypothesis of outlier test.

Details

The function computes the estimated proportion of outliers (gauge) based on impulse indicator saturation and constructs the proportion and count outlier test statistics from Jiao and Pretis (2019). The null hypothesis is that the proportion (or count) of outliers is not different than the proportion (or count) of outliers detected under the null hypothesis of no outliers. The first test compares the estimated proportion of outliers scaled by its estimated variance against a standard normal distribution. The second test compares the number of outliers against a Poisson distribution. If an isat object is provided in x, then the function automatically extracts the detected impulses and computes the estimated outlier proportion. If no isat object is provided and x=NULL, then the tests can be conducted manually by providing the number of detected outliers (noutl), the sample size (T), and the chosen level of signficance used to detect outliers (t.pval).

Value

Returns a list of two htest objects. The first providing the results of the test on the proportion of outliers against a standard normal distribution. The second providing the results on the number of outliers against the Poisson distribution.

References

Jiao, X. & Pretis, F. (2019). Testing the Presence of Outliers in Regression Models. Discussion Paper.

Pretis, F., Reade, J., & Sucarrat, G. (2018). Automated General-to-Specific (GETS) regression modeling and indicator saturation methods for the detection of outliers and structural breaks. Journal of Statistical Software, 86(3).

Author

Xiyu Jiao, & Felix Pretis, http://www.felixpretis.org/

Examples

  ###Testing the Presence of Outliers in the Nile Data
  nile <- as.zoo(Nile)
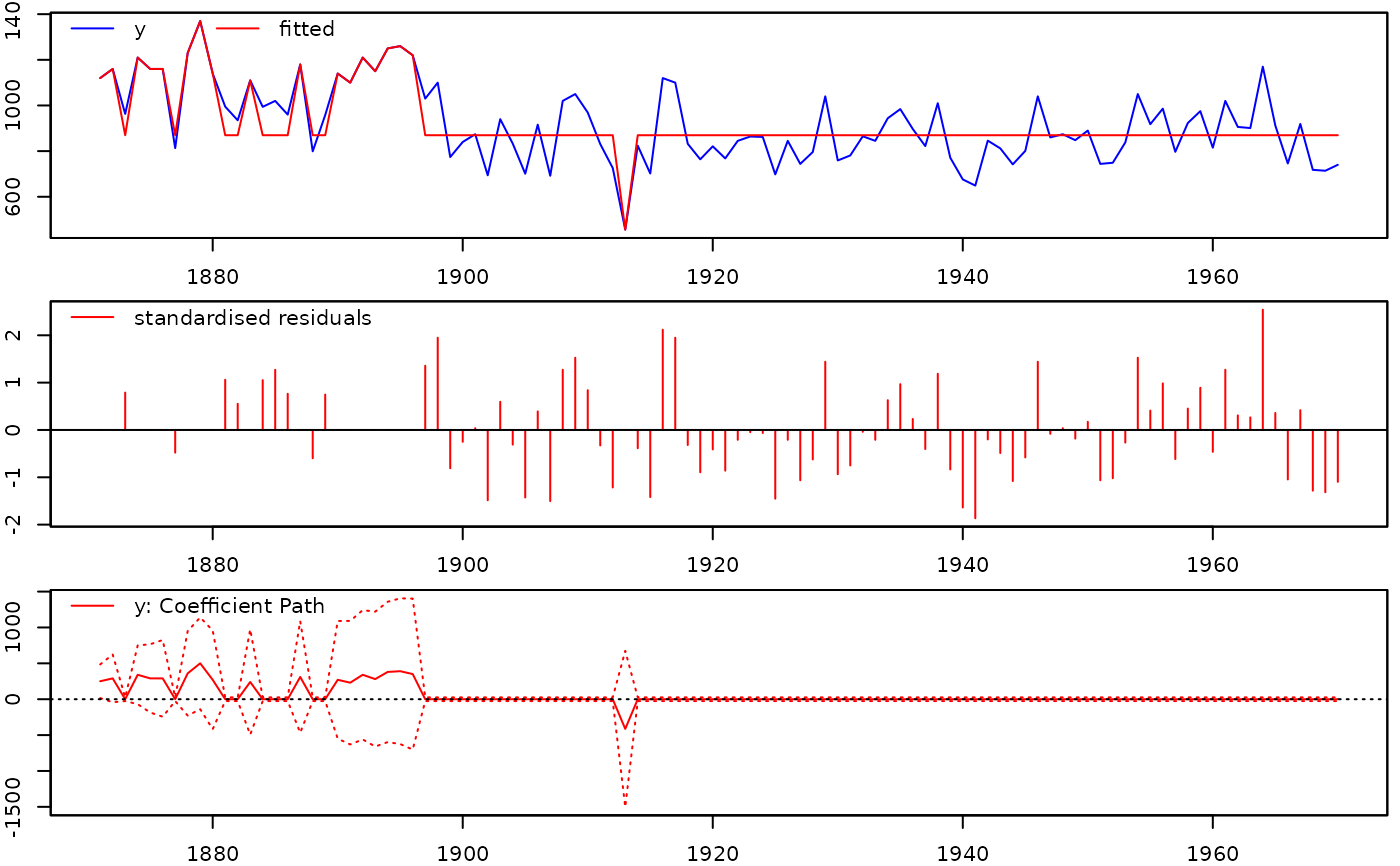
  isat.nile <- isat(nile, sis=FALSE, iis=TRUE, plot=TRUE, t.pval=0.1)
#> 
#> IIS block 1 of 4:
#> 9 path(s) to search
#> Searching: 
#> 1 
#> 2 
#> 3 
#> 4 
#> 5 
#> 6 
#> 7 
#> 8 
#> 9 
#> 
#> IIS block 2 of 4:
#> 23 path(s) to search
#> Searching: 
#> 1 
#> 2 
#> 3 
#> 4 
#> 5 
#> 6 
#> 7 
#> 8 
#> 9 
#> 10 
#> 11 
#> 12 
#> 13 
#> 14 
#> 15 
#> 16 
#> 17 
#> 18 
#> 19 
#> 20 
#> 21 
#> 22 
#> 23 
#> 
#> IIS block 3 of 4:
#> 24 path(s) to search
#> Searching: 
#> 1 
#> 2 
#> 3 
#> 4 
#> 5 
#> 6 
#> 7 
#> 8 
#> 9 
#> 10 
#> 11 
#> 12 
#> 13 
#> 14 
#> 15 
#> 16 
#> 17 
#> 18 
#> 19 
#> 20 
#> 21 
#> 22 
#> 23 
#> 24 
#> 
#> IIS block 4 of 4:
#> 25 path(s) to search
#> Searching: 
#> 1 
#> 2 
#> 3 
#> 4 
#> 5 
#> 6 
#> 7 
#> 8 
#> 9 
#> 10 
#> 11 
#> 12 
#> 13 
#> 14 
#> 15 
#> 16 
#> 17 
#> 18 
#> 19 
#> 20 
#> 21 
#> 22 
#> 23 
#> 24 
#> 25 
#> 
#> GETS of union of retained IIS variables... 
#> 
#> GETS of union of ALL retained variables...
#> - All non-keep regressors significant in GUM

  outliertest(isat.nile)
#> $proportion
#> 
#> 	Jiao-Pretis Outlier Proportion Test
#> 
#> data:  Proportion of detected outliers
#> = 4.4415, p-value = 8.932e-06
#> alternative hypothesis: true  is not equal to 0.1
#> sample estimates:
#> [1] 0.18
#> 
#> 
#> $count
#> 
#> 	Jiao-Pretis Outlier Count Test
#> 
#> data:  Number of detected outliers
#> = 18, p-value = 0.01705
#> alternative hypothesis: true  is not equal to 10
#> sample estimates:
#> [1] 18
#> 
#> 
  
  ###Testing the number of outliers when the sample is T=200, 
  ### with 7 detected outliers at t.pval=0.05 if no isat object is provided:
  outliertest(x=NULL, noutl=7, t.pval=0.05, T=200)
#> $proportion
#> 
#> 	Jiao-Pretis Outlier Proportion Test
#> 
#> data:  Proportion of detected outliers
#> = -1.455, p-value = 0.1457
#> alternative hypothesis: true  is not equal to 0.05
#> sample estimates:
#> [1] 0.035
#> 
#> 
#> $count
#> 
#> 	Jiao-Pretis Outlier Count Test
#> 
#> data:  Number of detected outliers
#> = 7, p-value = 0.4287
#> alternative hypothesis: true  is not equal to 10
#> sample estimates:
#> [1] 7
#> 
#>